Problem 5: Insect Combinatorics (200pts)
Problem
Consider an insect in an
MbyNgrid. The insect starts at the bottom left corner,(0, 0), and wants to end up at the top right corner,(M-1, N-1). The insect is only capable of moving right or up by one step (e.g., from(0, 0)to(0, 1)or(1, 0)).Write a function
pathsthat takes a grid's lengthMand widthNas input, thenpathsis supposed to return the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)
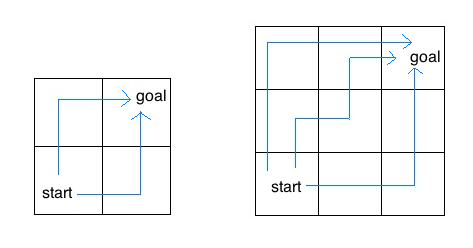
For example, a 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For a 3 by 3 grid, the insect has 6 different paths (only 3 are shown above).
考虑一只昆虫在一个 M 乘 N 的网格中。昆虫从左下角的 (0, 0) 出发,想要到达右上角的 (M-1, N-1)。昆虫每次只能向右或向上移动一步(例如,从 (0, 0) 移动到 (0, 1) 或 (1, 0))。
编写一个函数 paths,它接受网格的长度 M 和宽度 N 作为输入,然后 paths 应该返回昆虫可以从起点到终点采取的不同路径的数量。(这个问题有一个 闭合形式 的解,但请尝试使用递归以程序化的方式来回答。)
例如,一个 2 乘 2 的网格总共有两种方式让昆虫从起点移动到终点。对于一个 3 乘 3 的网格,昆虫有 6 条不同的路径(上面只显示了 3 条)。
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
Hints
-
这类题在小学很常见,想想怎么实现。
-
base case 的 0 和 1 不要写错了。
Solutions
base case: 只要 m 和 n 有一个为 1,那么 paths(m, n) 的返回值为 1。
def paths(m, n):
if m == 1 or n == 1:
return 1
else:
return paths(m - 1, n) + paths(m, n - 1)